Re: Can a decay curve of a radioactive substance ever reach 0?

Be sure to visit our archives using our search engine to search on "radioactive decay". In many of the previous answers you will find equations for determining the "decay constant" and halflife of radioactive particles. The decay constant, L, is
L = ln(2) / T_1/2
where T_1/2 is the halflife and "ln" is the natural logarithm, with ln(2) being about 0.693. After the decay constant is found, the equation for the number of particles, N, after a certain time, T, is
N = N_o e^-LT
where N_o is the number of particles at time T=0.

Here is a picture of an Excel chart containing the data you sent, along with an exponential trendline that is the best fit to your data:

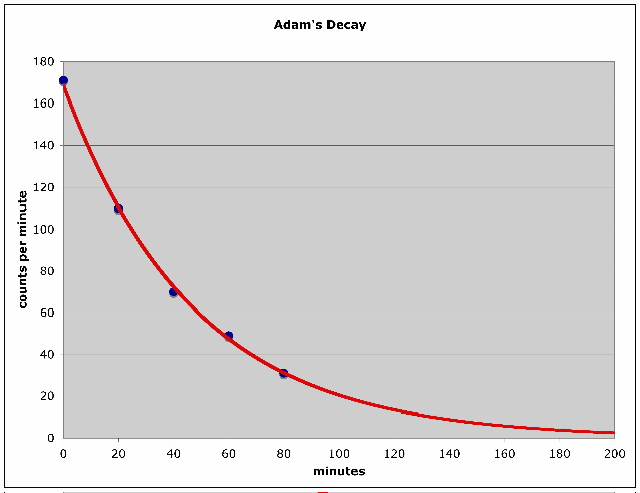
From these data Excel computes a decay constant of 0.0211 per minute and an N_o equal to 168.7, from which the halflife can be computed as 32.9 minutes. Let's calculate the number of particles at T=1440 minutes (24 hours):
N = 168.7 e^-0.0211*1440 = 1.1E-11
which is reasonably close to your calculation of 1.6E-11. But things are not so clean when we are dealing with small numbers of particles, and, indeed, is there even such a thing as a fraction of a particle? The answer to that question is "no" and accounts for the fact that your teacher is correct in saying there will be zero particles after 24 hours. Starting at 171 particles there is only 1 particle left after about 7 halflives. 24 hours is 43.8 halflives, so the one remaining particle would have to not decay after about 36 or so halflives! While there is a finite probability of that happening, the probability is extremely small, so it is safe to say that at the end of the 24 hours the number of particles left will be zero.

The probability of any one particle not decaying after a time of one halflife is 50% (0.5). You can verify that by thinking of starting with, say, 4 particles. After one halflife, on average, 2 will have decayed. So after one halflife only 50% of the particles decayed. When we get down to only 1 particle left there's a 50% chance (0.5) that it will not decay before one halflife is ended. If it does not decay after that time, there's still only a 50% chance that it will not decay after an additional halflife time, so that after 2 halflives there is only a 25% chance (0.5 * 0.5) that it will not have decayed. In your problem the one particle has about 36 halflives to get through without decaying, which means that the chance of that happening is
0.5³⁶ = 1.5E-11 = 1.5E-9%. That is a small enough probability to accept the fact that that single particle will not be there at the end of the 24 hours.

John Link, MadSci Physicist