Figure 1
| MadSci Network: Physics |
Diffraction gratings are devices which can cause heaps and heaps of confusion for school students and university researchers alike. Mostly this confusion comes from how the so-called "grating equation" is used.
The problem is that a diffraction grating can be used in many ways and the equation can be simplified in different ways depending on the situation.
HOWEVER, one equation always holds regardless of whether the grating used is a transmission grating (i.e. the light is diffracted as it passes through the grating), a reflection grating (i.e. the light is diffracted as it is reflected from the surface of the grating) or even if the grating is something special a the blazed grating used for serious spectroscopic studies. This is the equation:
m λ = d (sin(θi) + sin(θm)) .............. (1)
Where m is the order of the diffraction, λ is the wavelength of the light, d is the groove spacing, θi is the angle of incidence and θm is the diffraction angle.

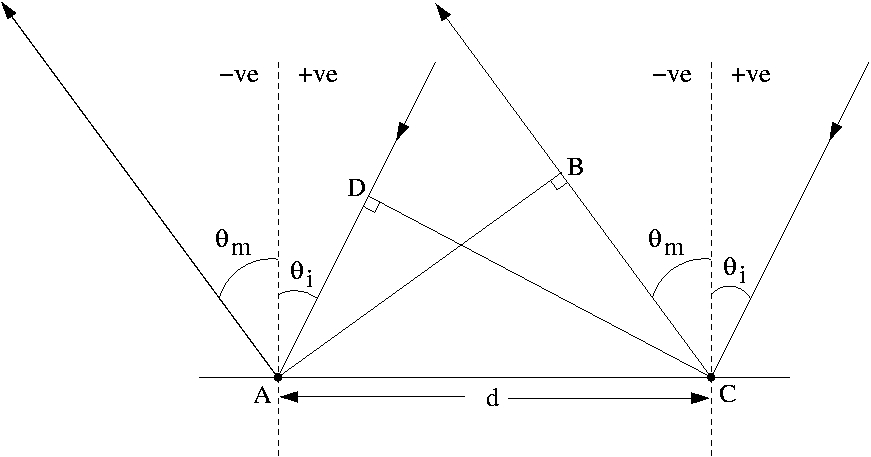
Figure 1
This is shown in diagram 1 where the relative phase-difference between the wave coming in from the right hand side and the diffracted wave going out towards the left hand side gives the condition for diffraction. The phase difference is given by the adding up the lengths BC and AD. Using trigonometry you can work out that BC = d sin(θm) and AD = d sin(θi). If we add these together the result has to be a multiple of the wavelength that we are considering. This condition is written in the equation as mλ, where m is an integer (a whole number). This gives us equation (1).
If we put into the grating equation above that θi = 0 we find that, since sin(0) = 0:
m λ = d sin(θm) .............. (2)
This is, by far, the most common form of the grating equation seen. This situation is shown in diagram number 2.
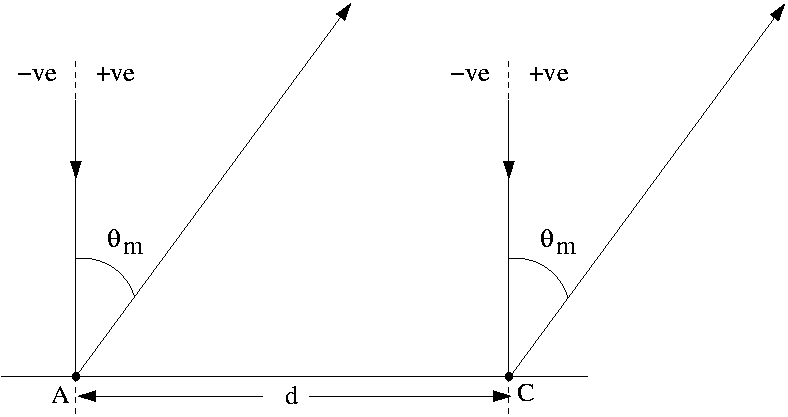
Figure 2
m λ = d sin(θm) .............. (3)
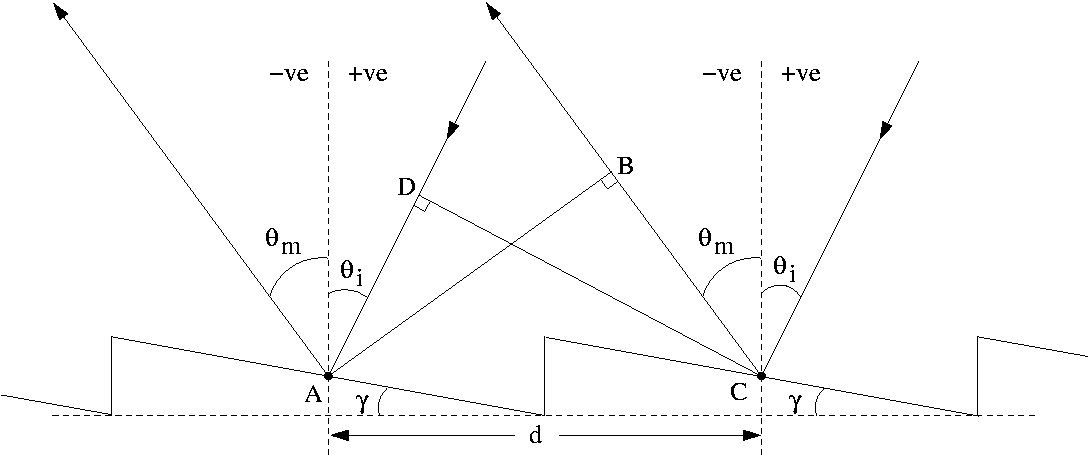
Figure 3
This situation is shown in diagram 3. The only difference between a blazed grating and a "plane" grating is that, since the grating is blazed (tilted) at an angle of γ most light, when it is incident along the normal to the grating (shown as the dotted line on the picture), gets diffracted in the direction where θm = 2γ. This makes this type of grating more efficient when performing spectroscopy.
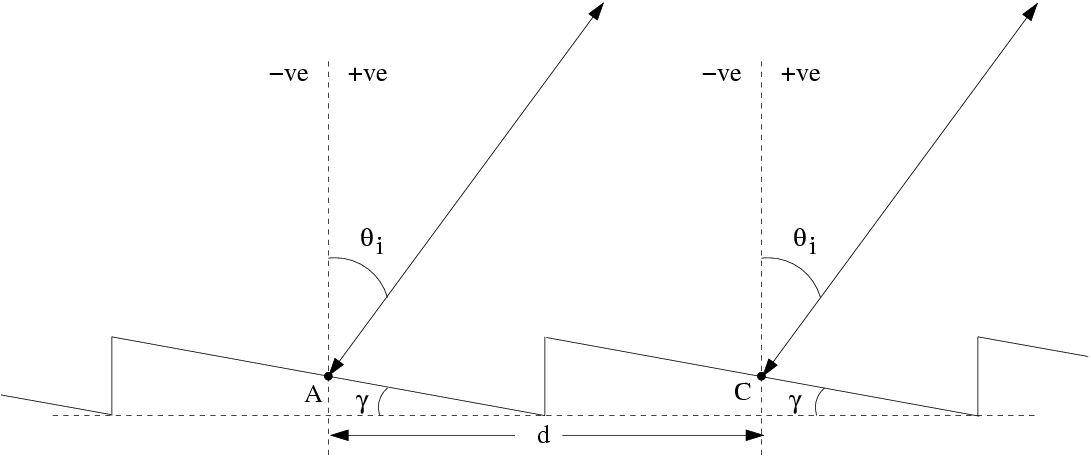
Figure 4
In this case, since θi and θm are equal, the grating equation simplifies to:
m λ = 2 d sin(θm) .............. (4)
Which is very similar to the equation (2) we had for diffraction when the angle of incidence was zero, but now with a factor of 2! This is a major source of confusion. To know which equation to use you have to know exactly which type of experiment you are trying to describe.
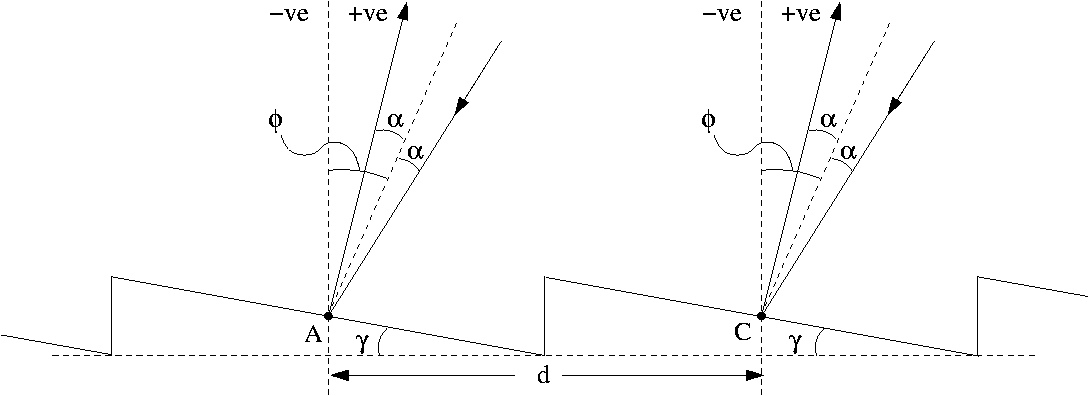
Figure 5
In this situation it is normal to play around a little with the angles to make the equation simpler. Now, as shown in the diagram, we define an angle between the normal to the grating and a direction halfway between the incident and diffracted beams and call this φ. This will be the angle of the grating in the spectrometer which is changed by turning a knob (so this is something we can adjust when making measurements).
The other two important angles are those between the direction we just defined and the the angle of incidence, θi, and the diffraction angle, θm. Since our direction defined by φ is halfway between the two, we can call this angle α. Now the angle between θm and θi is then just 2α (hopefully, this is clear from the diagram).
If you are a bit puzzled about this, we have just done a little bit of cheating by adding and subtracting angles to give us two new angles, but since we started with two angles, θm and θi, and have ended up with two angles, φ and α, it is all okay (promise). Staring at the diagram and drawing a lot of big pictures of your own will help to convince you.
We can now write down equations for φ and α in terms of θm and θi:
φ = (θi + θm)/2 .............. (5)
α = (θi - θm)/2 .............. (6)
The is where it gets a bit mathematical. We can see from the diagram that θi is equal to φ + α and θm is equal to φ + α so we can just put these back into the diffraction equation (1) and we get:
m λ = d (sin(φ + α) + sin(φ - α)) .............. (7)
Now, there is a fairly well-known equation in trigonometry which says that we can rewrite such expressions in the following way:
2 sin(A)cos(B) = sin(A+B) + sin(A-B) .............. (8)
So rewrite equation (7) as:
m λ = 2 d sin(φ) cos(α) .............. (9)
Now, if you were not confused enough, we can make an extra simplification to this equation. Since, in most spectrometers α ≈ 0 (the angle between the incident beam and diffracted beam is very small), we can simplify equation (9) to be just
m λ = 2 d sin(φ) .............. (10)
which again looks like equation (4) and double equation (2) so, again, be warned that you have to know exactly which kind of setup you want to describe because, if you use the wrong equation, your answer is likely to be two times too big or two times too small!
More information about diffraction gratings can be found at the Grating Lab website and the Jobin Yvon website, which are both companies who make diffraction gratings and spectrometers for science and engineering.
I am sure there must be books with well-described sections on diffraction gratings out there somewhere, but I have yet to find one. If someone can recommend a good, simple book on this subject I would be very interested.
Happy diffracting!
Try the links in the MadSci Library for more information on Physics.