| MadSci Network: Physics |
Hi Pam,
The answer to your question is yes, there's definitely a connection between quadratic equations and rockets. There are some complications when you deal with actual toy rockets, and I'll try to point those out.
First some basics on projectiles and quadratics (if you know all this skip ahead). Newton figured out that for objects of fixed mass, the acceleration of an object is related to the force on the object by
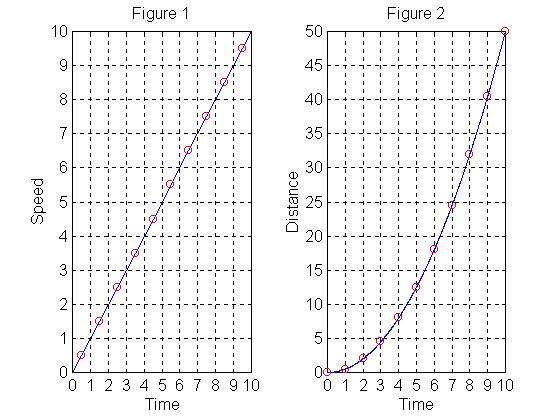
Acceleration is the rate of change of speed with time. If the force on an object is constant, then the acceleration is constant, and a graph of of speed vs. time has constant slope--a line (Figure 1). For each interval of time, you can take the average speed (the circles in Figure 1) and determine how far the object went in that interval. So if an object starts with speed zero and increases its speed one meter per second each second, then it goes 0.5 meters in the first second, 1.5 meters in the second second, 2.5 in the third, etc. If you add these as you go, you get the total distance as a function of time--which turns out to be a quadratic function (Figure 2). If you get them started and point them in the right direction, your students can "discover" this parabola for themselves.

With that figured out, you might (for example) write out the general quadratic equation,
I recently saw a toy rocket for sale which is made of a soft, Nerf-like material. It sits on a straw-like thing connected to a rubber ball. When you stomp on the rubber ball, air is forced through the straw and the rocket zooms up 20-30 feet. Once the rocket leaves the straw, the only force on it is gravity, so a is -9.8 m/s² (negative since the rocket is going up but gravity gives a downward acceleration). Many other toy "rockets" work the same way: if you throw, slingshot, catapault, or otherwise launch something that doesn't carry its own propulsion, then immediately after launch, the only force on the object is gravity (neglecting air friction--see below). For all such devices, if the ground is d=0, then you can measure the height d (since the rocket is moving vertically, "distance" now means height) vs. time and solve for the initial velocity.
How do you measure the height? There's a trivial way: at the time the rocket hits the ground again, you know its height is zero, so you don't have to measure it. The time the rocket hits the ground gives you a time/height pair, which you can plug into the equation to solve for b.
But how could you measure the maximum height reached by the rocket? Well, one way is to consider the rocket from the top of its flight, right as it starts to fall again. >From that point it has an initial position (the unknown height), zero initial velocity, and the acceleration is just gravity. So if you know the time it takes to get from the top of its path back to the ground, you can solve for the height. You might see if your students can come up with that (or other methods of height measurement!) on their own before suggesting it to them!
So far we've been talking about rockets which go only straight up and down. If the rocket is aimed at an angle e, then the thrust will be in the direction the rocket is facing. Thus it will have a horizontal component (F cos e), and a vertical component (F sin e). These two components act completely separately, and the horizontal and vertical position of the rocket with time can be worked out independently.
Of course, gravity eventually brings the rocket to the ground, and the rocket will only get as far horizontally as it has time to before this happens. A time-tested exercise is to have your students guess, and then prove, what angle is best to make the rocket go farthest. While an analytical derivation is a calculus problem, your students could determine an equation for horizontal distance vs. launch angle, plot it, and see where it was maximum, then test their findings with the toy rockets. This is a good excercise for review of quadratics in a trig class, or review of basic trig in an Algebra II class, depending on which order you teach them in.
Ok: now assume a rocket takes off (straight up) with its engines burning constantly from t=0 to some ending time T. If we assume the burning fuel doesn't change the mass very much, and that the force from the engine stays the same the whole time the engine is burning, then during that time, a is the acceleration due to the rocket plus that due to gravity (that is, minus 9.8 m/s²). When the engine shuts off or burns out, a switches to just gravity. Then the rocket starts to slow down until it reaches zero speed at the top of its path, at which point it starts to fall again. From there, you can again calculate the maximum height by measuring the fall time.
You can also measure the amount of time it takes the rocket to get to its maximum height. If you do that, still keeping our assumptions, do you have enough information to calculate the force of the engine? (A: only if you know how long the engine burns!) Can you backtrack and recreate the height as a function of time? Is it still a parabola? (A: No, it's not a parabola, because the acceleration was not constant! But under our assumptions, it was a constant for a while, and then suddenly a different constant, so the graph is a parabola whose parameters suddenly change. One good excercise might be for students to predict the way the curve changes when the engine shuts off.)
I don't know if, in a genuine model rocket (with a burning fuel cell ignited by an electric starter), the fuel provides constant thrust (force). Further, as the fuel burns, the mass of the rocket changes. In any case the acceleration due to the engine is probably not constant. This fact is important in real rockets--see the Mad Scientist Network posting about space travel and the Jet Propulsion Laboratory's page on space travel basics. But it complicates the toy rocket problem. Also, wind and air friction are likely to cause additional decelerations on the rocket.
If you ignore air effects and do the calculations as if the engine force were constant, you will come up with an "average force" which, if it were true, would have produced the same effect as the real engine. Maybe your class can come up with a way to test by experiment whether the force of the engine is approximately constant, or not!
One thing you might hear is that the path of a rocket is itself shaped like a parabola. This is only true in particular circumstances: if the horizontal speed of the rocket is constant, then the horizontal distance and time are linearly related. A graph of height vs. time will look just like a plot of height vs. horizontal distance, just with different units on the x-axis--in other words, a parabola. But a real toy rocket, as we've discussed, has air resistance and wind to change its horizontal speed in flight, and if it's burning its own engine, then that also provides horizontal acceleration. It might be a good excercise for your students to plot, for the accelerating rocket, horizontal distance vs. time, vertical distance vs. time, and then horizontal distance vs. vertical distance. This is a good, simple example of a parametric curve, and shows that the rocket path is "parabola-looking" but not parabolic. To prove it, you could work out the ideal case of the accelerating rocket (ignore air effects), plot the path, and then try and fit a parabola (y = ax²+bx+c) to the points on the plot. You might try and predict the distortion from a true parabola as a function of the launch angle. Are there any angles where the path becomes a parabola again?
This issue becomes more complicated for a real toy rocket, which, if launched at an angle, might change its angle relative to the ground as it goes. Then the individual horizontal and vertical thrust components are constantly changing, making the various changes hard to keep track of without calculus.
Final note, in case you are using real model rockets and haven't used them before, keep in mind that they can be dangerous. Lots of information about model rockets can be found on the web by searching the web for "model rocket".
Good luck!
Dan Goldner (goldner@mit.edu)
MIT/Woods Hole
Joint Program in
Oceanography
Try the links in the MadSci Library for more information on Physics.