Date: Tue May 11 23:52:57 1999
Posted By: Eric George, Other (pls. specify below), Aerospace Engineer, Nichols Research Corp.
Area of science: Physics
ID: 925756435.Ph
Message:
Hi,
I think your question boils down to derivatives of the equations of
motion. Yourequested a non-calculus based method, but calculus is really
at the heart of it, so I'll give you a quick rundown on that as well.
Let's consider a one-dimensional system where the position of a point
can be expressed as X. A point moving along a straight line is a good
example.
Position = X
The velocity of the point is the rate of change of position with respect
to time.
Velocity = (X2 - X1)/(T2 - T1)
where X2 is the point's position at time T2 and X1 is the point's
position at time T1
The problem with this formula is that the velocity of the object might
be changing between T1 and T2 so the result will be an average
velocity.
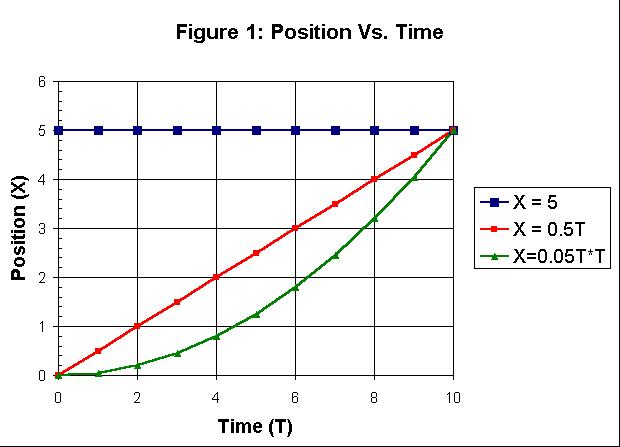
For example, in figure 1 if you pick T1 = 0 and T2 = 10 for the interval,
you will get the same value for the velocity for the green line and the
red line although this is not really true as we'll soon see.
This is where the calculus comes in...
 The true definition of velocity is that it is the derivative of the
position with respect to time. What this means is that you find the
limit of the velocity equation as your time interval goes to zero.
V = (X2 - X1)/(T2 - T1) as (T2-T1) approaches zero.
Another way to look at this is that velocity is the slope of the position
vs. time curve.
The true definition of velocity is that it is the derivative of the
position with respect to time. What this means is that you find the
limit of the velocity equation as your time interval goes to zero.
V = (X2 - X1)/(T2 - T1) as (T2-T1) approaches zero.
Another way to look at this is that velocity is the slope of the position
vs. time curve.
 The way to write this is:
V = dX/dT where d means delta or small change.
Here are some derivatives of some simple polynomial terms, you'll see where
they come from when you take calculus:
X = 5 -> dX/dT = 0
(X is not a function of T so it's rate of change wrt T is zero)
X = T -> dX/dT = 1
X = T*T = T^2 -> dX/dT = 2T
X = T*T*T = T^3 -> dX/dT = 3T^2
The rule for derivative of products is:
X = Y*Z -> dX/dT = Y*dZ/dT + Z*dY/dT
So, if the position of your particle as a function of time can be expressed as
X = 0.05*T^2
then
V = 0.05*2*T + 0*T^2 = 0.05*2*T = 0.1T
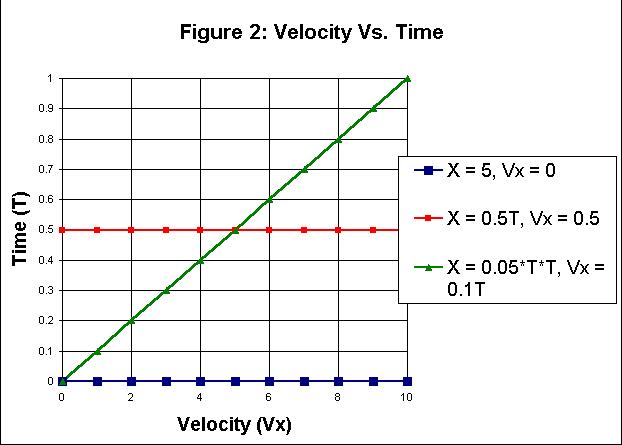
This is the green line in figures 1 and 2.
I'm sure you already know this from your physics classes, don't worry, I'm
getting to your question!
The equations of motion continue this way ad infinitum...
Acceleration = A = dV/dT = d^2X/dT^2
(d^2X/dT^2 means the second derivative of X with respect to T)
The derivatives beyond acceleration, which you called triceleration and
tetraceleration, aren't commonly named as far as I know. But they are important!
Again the pattern is the same...
"Triceleration" units of m/s^3
Q = dA/dT = d^2V/dT^2 = d^3X/dT^3
"Tetraceleration" units of m/s^4
dQ/dT = d^2A/dT^2 = d^3V/dT^3 = d^4X/dT^4
Here is an examples of where higher derivatives of acceleration are important.
Say you have a rocket that masses 1000 kg and produces a thrust of 100 Newtons
and burns 10 kg of fuel per second.
Newtons Law states that Force = Mass * Acceleration
We can solve for A = F/M
and we also know that mass is a function of time:
M = 1000 - 10*T Kg
so that
A = F/(1000 - 10*T)
Now your "triceleration" is equal to
Q = dA/dT = 10*F/100 = 0.1F
Note that this is a positive value. This means that the acceleration of the
rocket increases with time, which should make sense to you.
Using another calculus operation known as integration (which I don't have
time to explain tonight...sorry) we could also find the position and velocity
of the rocket as a function of time.
I hope this helps, here are some good links on calculus that might help also.
http://www.math.utep.edu/sosmath/
http://web.mit.edu/wwmath/calculus/summary.html
http://www.netsrq.com/~hahn/calculus.html
Note that through this whole thing I am not dealing with motion in a
gravitational field. That would add and acceleration term as a function of
position.
Good luck with the Astrophysics!
Eric
The way to write this is:
V = dX/dT where d means delta or small change.
Here are some derivatives of some simple polynomial terms, you'll see where
they come from when you take calculus:
X = 5 -> dX/dT = 0
(X is not a function of T so it's rate of change wrt T is zero)
X = T -> dX/dT = 1
X = T*T = T^2 -> dX/dT = 2T
X = T*T*T = T^3 -> dX/dT = 3T^2
The rule for derivative of products is:
X = Y*Z -> dX/dT = Y*dZ/dT + Z*dY/dT
So, if the position of your particle as a function of time can be expressed as
X = 0.05*T^2
then
V = 0.05*2*T + 0*T^2 = 0.05*2*T = 0.1T
This is the green line in figures 1 and 2.
I'm sure you already know this from your physics classes, don't worry, I'm
getting to your question!
The equations of motion continue this way ad infinitum...
Acceleration = A = dV/dT = d^2X/dT^2
(d^2X/dT^2 means the second derivative of X with respect to T)
The derivatives beyond acceleration, which you called triceleration and
tetraceleration, aren't commonly named as far as I know. But they are important!
Again the pattern is the same...
"Triceleration" units of m/s^3
Q = dA/dT = d^2V/dT^2 = d^3X/dT^3
"Tetraceleration" units of m/s^4
dQ/dT = d^2A/dT^2 = d^3V/dT^3 = d^4X/dT^4
Here is an examples of where higher derivatives of acceleration are important.
Say you have a rocket that masses 1000 kg and produces a thrust of 100 Newtons
and burns 10 kg of fuel per second.
Newtons Law states that Force = Mass * Acceleration
We can solve for A = F/M
and we also know that mass is a function of time:
M = 1000 - 10*T Kg
so that
A = F/(1000 - 10*T)
Now your "triceleration" is equal to
Q = dA/dT = 10*F/100 = 0.1F
Note that this is a positive value. This means that the acceleration of the
rocket increases with time, which should make sense to you.
Using another calculus operation known as integration (which I don't have
time to explain tonight...sorry) we could also find the position and velocity
of the rocket as a function of time.
I hope this helps, here are some good links on calculus that might help also.
http://www.math.utep.edu/sosmath/
http://web.mit.edu/wwmath/calculus/summary.html
http://www.netsrq.com/~hahn/calculus.html
Note that through this whole thing I am not dealing with motion in a
gravitational field. That would add and acceleration term as a function of
position.
Good luck with the Astrophysics!
Eric
Current Queue |
Current Queue for Physics |
Physics archives
Try the links in the MadSci Library for more information on Physics.
MadSci Home | Information |
Search |
Random Knowledge Generator |
MadSci Archives |
Mad Library | MAD Labs |
MAD FAQs |
Ask a ? |
Join Us! |
Help Support MadSci
MadSci Network,
webadmin@www.madsci.org
© 1995-1999. All rights reserved.
 The true definition of velocity is that it is the derivative of the
position with respect to time. What this means is that you find the
limit of the velocity equation as your time interval goes to zero.
V = (X2 - X1)/(T2 - T1) as (T2-T1) approaches zero.
Another way to look at this is that velocity is the slope of the position
vs. time curve.
The true definition of velocity is that it is the derivative of the
position with respect to time. What this means is that you find the
limit of the velocity equation as your time interval goes to zero.
V = (X2 - X1)/(T2 - T1) as (T2-T1) approaches zero.
Another way to look at this is that velocity is the slope of the position
vs. time curve.
 The way to write this is:
V = dX/dT where d means delta or small change.
Here are some derivatives of some simple polynomial terms, you'll see where
they come from when you take calculus:
X = 5 -> dX/dT = 0
(X is not a function of T so it's rate of change wrt T is zero)
X = T -> dX/dT = 1
X = T*T = T^2 -> dX/dT = 2T
X = T*T*T = T^3 -> dX/dT = 3T^2
The rule for derivative of products is:
X = Y*Z -> dX/dT = Y*dZ/dT + Z*dY/dT
So, if the position of your particle as a function of time can be expressed as
X = 0.05*T^2
then
V = 0.05*2*T + 0*T^2 = 0.05*2*T = 0.1T
This is the green line in figures 1 and 2.
I'm sure you already know this from your physics classes, don't worry, I'm
getting to your question!
The equations of motion continue this way ad infinitum...
Acceleration = A = dV/dT = d^2X/dT^2
(d^2X/dT^2 means the second derivative of X with respect to T)
The derivatives beyond acceleration, which you called triceleration and
tetraceleration, aren't commonly named as far as I know. But they are important!
Again the pattern is the same...
"Triceleration" units of m/s^3
Q = dA/dT = d^2V/dT^2 = d^3X/dT^3
"Tetraceleration" units of m/s^4
dQ/dT = d^2A/dT^2 = d^3V/dT^3 = d^4X/dT^4
Here is an examples of where higher derivatives of acceleration are important.
Say you have a rocket that masses 1000 kg and produces a thrust of 100 Newtons
and burns 10 kg of fuel per second.
Newtons Law states that Force = Mass * Acceleration
We can solve for A = F/M
and we also know that mass is a function of time:
M = 1000 - 10*T Kg
so that
A = F/(1000 - 10*T)
Now your "triceleration" is equal to
Q = dA/dT = 10*F/100 = 0.1F
Note that this is a positive value. This means that the acceleration of the
rocket increases with time, which should make sense to you.
Using another calculus operation known as integration (which I don't have
time to explain tonight...sorry) we could also find the position and velocity
of the rocket as a function of time.
I hope this helps, here are some good links on calculus that might help also.
http://www.math.utep.edu/sosmath/
http://web.mit.edu/wwmath/calculus/summary.html
http://www.netsrq.com/~hahn/calculus.html
Note that through this whole thing I am not dealing with motion in a
gravitational field. That would add and acceleration term as a function of
position.
Good luck with the Astrophysics!
Eric
The way to write this is:
V = dX/dT where d means delta or small change.
Here are some derivatives of some simple polynomial terms, you'll see where
they come from when you take calculus:
X = 5 -> dX/dT = 0
(X is not a function of T so it's rate of change wrt T is zero)
X = T -> dX/dT = 1
X = T*T = T^2 -> dX/dT = 2T
X = T*T*T = T^3 -> dX/dT = 3T^2
The rule for derivative of products is:
X = Y*Z -> dX/dT = Y*dZ/dT + Z*dY/dT
So, if the position of your particle as a function of time can be expressed as
X = 0.05*T^2
then
V = 0.05*2*T + 0*T^2 = 0.05*2*T = 0.1T
This is the green line in figures 1 and 2.
I'm sure you already know this from your physics classes, don't worry, I'm
getting to your question!
The equations of motion continue this way ad infinitum...
Acceleration = A = dV/dT = d^2X/dT^2
(d^2X/dT^2 means the second derivative of X with respect to T)
The derivatives beyond acceleration, which you called triceleration and
tetraceleration, aren't commonly named as far as I know. But they are important!
Again the pattern is the same...
"Triceleration" units of m/s^3
Q = dA/dT = d^2V/dT^2 = d^3X/dT^3
"Tetraceleration" units of m/s^4
dQ/dT = d^2A/dT^2 = d^3V/dT^3 = d^4X/dT^4
Here is an examples of where higher derivatives of acceleration are important.
Say you have a rocket that masses 1000 kg and produces a thrust of 100 Newtons
and burns 10 kg of fuel per second.
Newtons Law states that Force = Mass * Acceleration
We can solve for A = F/M
and we also know that mass is a function of time:
M = 1000 - 10*T Kg
so that
A = F/(1000 - 10*T)
Now your "triceleration" is equal to
Q = dA/dT = 10*F/100 = 0.1F
Note that this is a positive value. This means that the acceleration of the
rocket increases with time, which should make sense to you.
Using another calculus operation known as integration (which I don't have
time to explain tonight...sorry) we could also find the position and velocity
of the rocket as a function of time.
I hope this helps, here are some good links on calculus that might help also.
http://www.math.utep.edu/sosmath/
http://web.mit.edu/wwmath/calculus/summary.html
http://www.netsrq.com/~hahn/calculus.html
Note that through this whole thing I am not dealing with motion in a
gravitational field. That would add and acceleration term as a function of
position.
Good luck with the Astrophysics!
Eric